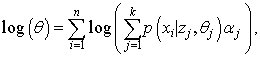詳細

一般的な形式の期待値最大化 (EM) アルゴリズム

X をパラメーター θ に応じて対数尤度 l(θ; X) になる観測値とします。X^m を潜在値または欠測値とすると、T=(X, X^m) は対数尤度 l₀ (θ; X) の完全なデータです。一般的な形式の問題を解くアルゴリズムは、次の EM アルゴリズム ([Dempster77]、[Hastie2009]) です。

1. パラメーター θ⁽⁰⁾ の初期値を選択します。

2. 期待値ステップ: j 番目のステップで、Q (θ', θ^(j)) = E (l₀ (θ'; T)|X, θ^(j)) を仮引数 θ' の関数として計算します。

3. 最大化ステップ: j 番目のステップで、θ' に対する Q(θ', θ^(j)) を最大化して、新しい推定 θ^(j+1) を計算します。

4. 収束するまでステップ 2 と 3 を繰り返します。

ガウス混合モデル用 EM アルゴリズム

ガウス混合モデル (GMM) は、以下のように表現される kd 次元多変量ガウス分布の混合モデルです。

ここで、Σ^k_{i = 1}α_i = 1 および α_i ≥ 0。

p( x|θ_i ) は、パラメーター θ_i = (m_i , Σ_i) の確率密度関数です。ここで、m_i は平均値ベクトル、Σ_i は分散共分散行列です。d 次元多変量ガウス分布の確率密度関数は、次のように定義されます。

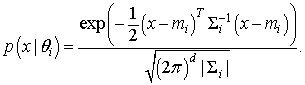
z_ij = I{x_i belongs to j mixture component} を指示関数、θ=(α₁, ..., α_k ; θ₁, ..., θ_k) とします。

次のように重みを定義します。

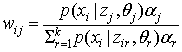
i=1, ..., n で j=1, …, k。

GMM の EM アルゴリズムには以下のステップが含まれます。

1. パラメーターの初期値を選択します。

   
   

2. 期待値ステップ: j 番目のステップで、行列 W = (w_ij)_nxk を重み w_ij で計算します。

3. 最大化ステップ: j 番目のステップで、r=1, ..., k について以下の項目を計算します。

   1. 混合重み

      

      ここで、

      

      は、r 番目の混合コンポーネントに割り当てられる特徴ベクトルの量 (amount)。

   2. 平均値推定

      
      

   3. 共分散推定

      
      サイズ d x d

      
      

4. 以下のいずれかの条件が満たされるまでステップ 2 と 3 を繰り返します。

   • 

     ここで、尤度関数は次のようになります。

     
     

   • 反復数が事前に定義されたレベルを超えた。