詳細

次元 p の n 特徴ベクトル x₁= (x₁₁,…,x_1p), ..., x_n= (x_n1,…,x_np) と正の整数 k で、ゴール関数 (クラスター内の 2 乗和) を最小化する kp 次元のベクトル m₁,…,m_k を見つけます。

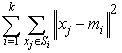
ここで、S_i は、m_i が最も接近した中心のベクトルのセットです。ベクトル m₁,…,m_k はセントロイドと呼ばれます。計算を開始するには、アルゴリズムにセントロイドの初期値が必要です。

セントロイド初期化は、以下の方法を使用して行います。

• データセットから k 特徴ベクトルをランダムに選択します。
• データセットから最初の k 特徴ベクトルを選択します。

目標関数の計算には、ベクトル間のユークリッド距離の計算 ||x_j- m_i|| が含まれます。アルゴリズムは、特徴ベクトル a と b の間のユークリッド距離: d(a,b) = d₁(a,b) + d₂(a,b) を使用します。ここで、d₁ は連続特徴の計算に使用されます。

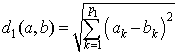
d₂ は二項カテゴリカル特徴の計算に使用されます。

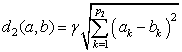
これらの式で、γ はクラスタリングの二項カテゴリカル特徴の影響の重み、p₁ は連続特徴の数、p₂ は二項カテゴリカル特徴の数です。アルゴリズムは非二項カテゴリカル特徴をサポートしないことに注意してください。

K 平均法アルゴリズムは、Lloyd メソッド [Lloyd82] を使用してセントロイドを計算します。各特徴ベクトル x₁,…,x_n で、特徴ベクトルを含むクラスターのインデックスを計算することもできます。